A Frequency Sampling Filter implementation. More...

#include <AsyncAudioFsf.h>

Inheritance diagram for Async::AudioFsf:

Public Member Functions
	AudioFsf (size_t N, const float *coeff, float r=0.99999)
	Default constructor.

	~AudioFsf (void)
	Destructor.

Public Member Functions inherited from Async::AudioProcessor
	AudioProcessor (void)
	Default constuctor.

virtual	~AudioProcessor (void)
	Destructor.

int	writeSamples (const float *samples, int len)
	Write audio to the filter.

void	flushSamples (void)
	Order a flush of all samples.

void	resumeOutput (void)
	Resume output to the sink if previously stopped.

void	allSamplesFlushed (void)
	All samples have been flushed by the sink.

Public Member Functions inherited from Async::AudioSink
	AudioSink (void)
	Default constuctor.

virtual	~AudioSink (void)
	Destructor.

bool	registerSource (AudioSource *source)
	Register an audio source to provide samples to this sink.

void	unregisterSource (void)
	Unregister the previously registered audio source.

bool	isRegistered (void) const
	Check if an audio source has been registered.

AudioSource *	source (void) const
	Get the registered audio source.

Public Member Functions inherited from Async::AudioSource
	AudioSource (void)
	Default constuctor.

virtual	~AudioSource (void)
	Destructor.

bool	registerSink (AudioSink *sink, bool managed=false)
	Register an audio sink to provide samples to.

void	unregisterSink (void)
	Unregister the previously registered audio sink.

bool	isRegistered (void) const
	Check if an audio sink has been registered.

AudioSink *	sink (void) const
	Get the registered audio sink.

bool	sinkManaged (void) const
	Check if the sink is managed or not.

void	handleAllSamplesFlushed (void)
	The registered sink has flushed all samples.

Protected Member Functions
virtual void	processSamples (float dest, const float src, int count)
	Process incoming samples and put them into the output buffer.

Protected Member Functions inherited from Async::AudioProcessor
void	setInputOutputSampleRate (int input_rate, int output_rate)
	Set the input and output sample rates.

Protected Member Functions inherited from Async::AudioSink
void	sourceResumeOutput (void)
	Tell the source that we are ready to accept more samples.

void	sourceAllSamplesFlushed (void)
	Tell the source that all samples have been flushed.

bool	setHandler (AudioSink *handler)
	Setup another sink to handle the incoming audio.

void	clearHandler (void)
	Clear a handler that was previously setup with setHandler.

AudioSink *	handler (void) const

Protected Member Functions inherited from Async::AudioSource
int	sinkWriteSamples (const float *samples, int len)

void	sinkFlushSamples (void)

bool	setHandler (AudioSource *handler)
	Setup another source to handle the outgoing audio.

AudioSource *	handler (void) const

void	clearHandler (void)
	Clear a handler that was previously setup with setHandler.

Detailed Description

A Frequency Sampling Filter implementation.

Author: Tobias Blomberg / SM0SVX

Date: 2018-01-03

This class implements a frequency sampling filter, FSF, as described in "Understanding Digital Signal Processing" by "Richard G. Lyons" third edition chapter 7.5. The variant that is implemented is the even 'N' real only variant with a modified type-IV resonator supporting the case I constellation. A frequency sampling filter is a FIR filter that consists of a cascade of comb filters and a number of recursive resonators. Even though this filter contains both non-recursive and recursive filters it has finate impulse response and linear phase characteristics so it can replace a standard FIR filter in some applications.

Even though an optimally designed Parks-McClellan FIR filter often have better performace in terms of stop band attenuation vs. transition bandwidth, the frequency sampling filter may be much more computationally efficient. As a rule of thumb, the frequency sampling filter is more computationally efficient than a PM-designed FIR filter when the passband is less than fs/5 and the transition bandwidth is less than fs/8, where fs is the sampling frequency.

The base of the FSF (frequency sampling filter) is formed by two cascaded comb filters. To define the frequency response of the filter, one or more resonators are added in parallel after the comb filters. Each resonator will pass frequencies falling within that "bin". The number of available bins are defined using the 'N' design parameter. The binwidth is fs/N. In the real-only case the bins 0 to N/2 can be used. The 'coeff' array is used to specify the stopband(s) and passbands(s). Simply put, a 0 designates the bin as a stopband and a 1 defines a passband. In reality values in between zero and one is often used to improve filter performance with transition band coefficients. These are not easily calculated so design tables are often used, like appendix H in the book mentioned initially.

Since the numeric precision in computers are finite a little tweak of the theory is required. A dampening factor is added to make the filter stable even though rounding errors are present. Whithout this dampening factor the filter poles may end up outside of the unit circle which would make the filter unstable. The drawback is that the filter will not have exactly linear phase but the approximation should be enough for most applications since it's very close to linear.

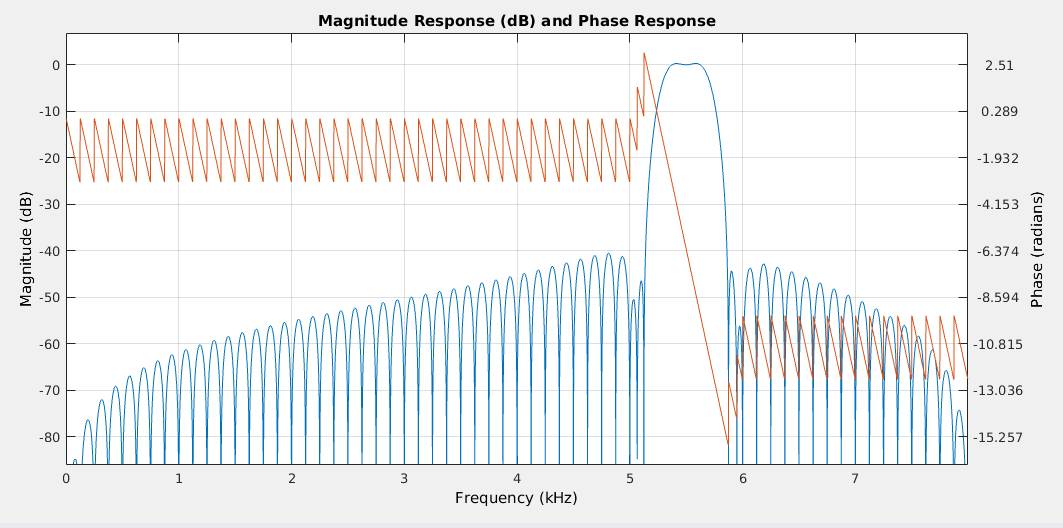
As a design example, let us assume we want a bandpass filter centered around 5500Hz with a 3dB bandwidth of about 400Hz. The sampling frequency is 16000Hz. The higher 'N' we choose, the more exact the passband will be in frequency and the narrowser the transition bandwidth will be. However, when choosing a high 'N' we also increase the number of resonators needed to cover the passband which increase the computational load. We thus like to keep 'N' as low as possible. In the example above we need a quite high 'N' to get a narrow passband that still have a flat frequency response so we choose N=128. To get the index of the center frequency we calculate 5500/(fs/N)=44. We thus set coeff[44]=1 and also do the same for coeff[43] and coeff[45] to get approximately the desired bandwidth. To improve the stopband attenutation (from like 15 to 40dB) we also need to add a couple of coefficients for the transition regions of the filter so we set coeff[42] and coeff[46]=0.39811024. That value has been looked up in the table mentioned above. All other positions must be set to 0 to form the stop band. The dampening factor 'r' should be left at its default unless there is a good reason to change it.

Example filter frequency response (blue) and phase response (red)

#include <iostream>
#include <cstring>
#include <cstdlib>
 
#include <AsyncCppApplication.h>
#include <AsyncAudioIO.h>
#include <AsyncAudioFsf.h>
 
// Read samples from the soundcard, filter it and then output it to the same
// soundcard
int main(int argc, const char **argv)
{
  Async::CppApplication app;
 
  Async::AudioIO::setSampleRate(16000);
  Async::AudioIO audio_io("alsa:plughw:0", 0);
  Async::AudioSource *prev_src = &audio_io;
 
    // A bandpass filter centered at 1000Hz with an approximate passband
    // bandwidth of 400Hz and a stopband attenuation of about 40dB.
  const size_t N = 128;   // N/fs=125Hz binwidth
  float coeff[N/2+1];
  std::memset(coeff, 0, sizeof(coeff));
  coeff[6] = 0.39811024;  // 750Hz
  coeff[7] = 1.0;         // 875Hz
  coeff[8] = 1.0;         // 1000Hz
  coeff[9] = 1.0;         // 1125Hz
  coeff[10] = 0.39811024; // 1250Hz
  Async::AudioFsf fsf(N, coeff);
  prev_src->registerSink(&fsf, true);
  prev_src = &fsf;
 
  prev_src->registerSink(&audio_io);
  prev_src = 0;
 
  if (!audio_io.open(Async::AudioIO::MODE_RDWR))
  {
    std::cout << "*** ERROR: Could not open audio device" << std::endl;
    exit(1);
  }
 
  app.exec();
 
  return 0;
}

Examples: AsyncAudioFsf_demo.cpp.

Definition at line 172 of file AsyncAudioFsf.h.

Constructor & Destructor Documentation

◆ AudioFsf()

Async::AudioFsf::AudioFsf	(	size_t	N,
		const float *	coeff,
		float	r = 0.99999 )

Default constructor.

Parameters

N	The number of filter "bins"
coeff	The N/2+1 coefficients defining the filter
r	The dampening factor

See class description for how to choose the argument values. The coeff array must have the length N/2+1 where coeff[0] is the filter section representing DC and the coeff[N/2] filter section represents fs/2. coeff[0] must be set to implement a lowpass filter and coeff[N/2] must be set to implement a highpass filter.

◆ ~AudioFsf()

Async::AudioFsf::~AudioFsf ( void )

Destructor.

Member Function Documentation

◆ processSamples()

virtual void Async::AudioFsf::processSamples	(	float *	dest,
		const float *	src,
		int	count )

protectedvirtual

Process incoming samples and put them into the output buffer.

Parameters

dest	Destination buffer
src	Source buffer
count	Number of samples in the source buffer

This function do the actual processing of the incoming samples.

Implements Async::AudioProcessor.

The documentation for this class was generated from the following file:

AsyncAudioFsf.h